Feasability study of wall shear stress imaging using microstructured surfaces with flexible micropillars

Abstract

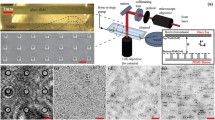
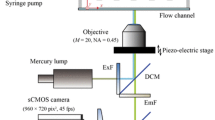
A new optical sensor technique based on a sensor film with arrays of hair-like flexible micropillars on the surface is presented to measure the temporal and spatial wall shear stress field in boundary layer flows. The sensor principle uses the pillar tip deflection in the viscous sublayer as a direct measure of the wall shear stress. The pillar images are recorded simultaneously as a grid of small bright spots by high-speed imaging of the illuminated sensor film. Two different ways of illumination were tested, one of which uses the fact that the transparent pillars act as optical microfibres, which guide the light to the pillar tips. The other method uses pillar tips which were reflective coated. The tip displacement field of the pillars is measured by image processing with subpixel accuracy. With a typical displacement resolution on the order of 0.2 μm, the minimum resolvable wall friction value is τ_w≈20 mPa. With smaller pillar structures than those used in this study, one can expect even smaller resolution limits.

Appendices

Appendix 1

Stokes’ drag force in an oscillating boundary layer flow

Unlike Oseen’s approximate quasi-steady solution, Stokes’ solution for a cylinder oscillating in a fluid accounts for oscillatory flow conditions and added mass effects. The drag force per unit length on the cylinder oscillating with velocity U(t)=U₀sin(ωt) is:

$$ f_{{\text{S}}} = {\left| {Z_{{\text{S}}} } \right|}{\kern 1pt} \cdot U_{0} \sin {\left( {\omega t + \zeta _{{\text{S}}} } \right)} $$

(6)

The quantity Z_S is the Stokes’ mechanical impedance and ζ_S is a phase shift, both of which are expressed by the following formulae:

$$ Z_{{\text{S}}} = Z_{{\text{R}}} + iZ_{{\text{I}}} = 4\pi \eta \cdot \frac{{ - g}} {{g^{2} + {\left( {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4} \right)}^{2} }} + i4\pi \eta \cdot {\left[ {\frac{{\omega D^{2} }} {{16\nu }} + \frac{{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}} {{g^{2} + {\left( {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4} \right)}^{2} }}} \right]} $$

(7)

$${\left| {Z_{{\text{S}}}} \right|} = {\sqrt {Z^{2}_{{\text{R}}} + \,Z^{2}_{{\text{I}}}}} ,$$

(8)

$$ \zeta _{S} = \tan ^{{ - 1}} {\left( {{Z_{{\text{I}}} } \mathord{\left/ {\vphantom {{Z_{{\text{I}}} } {Z_{{\text{R}}} }}} \right. \kern-\nulldelimiterspace} {Z_{{\text{R}}} }} \right)} $$

(9)

$$ g = 0.577 + \ln {\left( {{\sqrt {{\omega D^{2} } \mathord{\left/ {\vphantom {{\omega D^{2} } {16v}}} \right. \kern-\nulldelimiterspace} {16v}} }} \right)} $$

(10)

To take into account the velocity profile in the boundary layer of the sensor film, we use Stokes’ solution for the boundary layer of an oscillating flow with U(t)=U₀sin(ωt) at infinity above a flat plate yielding the following velocity profile:

$$ u{\left( {z,t} \right)} = U{\left( z \right)}\sin {\left( {\omega t + \xi _{{\text{S}}} {\left( z \right)}} \right)} $$

(11)

with:

$$ U{\left( z \right)} = U_{0} {\sqrt {{\left( {1 - {\text{e}}^{{ - \beta z}} \cdot \cos {\left( {\beta z} \right)}} \right)}^{2} + {\left( {{\text{e}}^{{ - \beta z}} \cdot \sin {\left( {\beta z} \right)}} \right)}^{2} } } $$

(12)

$$ \xi {\left( z \right)} = \tan ^{{ - 1}} {\left[ {{{\text{e}}^{{ - \beta z}} \sin {\left( {\beta z} \right)}} \mathord{\left/ {\vphantom {{{\text{e}}^{{ - \beta z}} \sin {\left( {\beta z} \right)}} {{\left( {1 - {\text{e}}^{{ - \beta z}} \cos {\left( {\beta z} \right)}} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - {\text{e}}^{{ - \beta z}} \cos {\left( {\beta z} \right)}} \right)}}} \right]} $$

(13)

$$ \beta = {\sqrt {\omega \mathord{\left/ {\vphantom {\omega {2v}}} \right. \kern-\nulldelimiterspace} {2v}} } $$

(14)

The actual force distribution on the pillars in the boundary layer is defined by the relative velocity u(z, t)−∂w/∂t, leading to the following expression of the force:

$$ f_{{\text{S}}} {\left( {z,t} \right)} = {\left| {Z_{s} {\left( z \right)}} \right|}{\left\{ {U{\left( z \right)}\sin {\left( {\omega t + \xi _{{\text{s}}} {\left( z \right)} + \zeta _{{\text{s}}} {\left( z \right)}} \right)} - \ifmmode\expandafter\dot\else\expandafter\.\fi{w}{\left( {z,{\left( {t + {\zeta _{{\text{s}}} {\left( z \right)}} \mathord{\left/ {\vphantom {{\zeta _{{\text{s}}} {\left( z \right)}} \omega }} \right. \kern-\nulldelimiterspace} \omega } \right)}} \right)}} \right\}} $$

(15)

Appendix 2

Frequency response of the pillars in the boundary layer

The response of the pillars to a certain oscillating force F(z, t), which is due to the viscous drag of the fluid moving around the pillars, is described by the one-dimensional Euler–Bernoulli differential equation. Following elastic theory, the governing equation (GE) of the motion of a uniform, homogeneous, one-side clamped cantilever beam with density ρ, cross-sectional area $$ \ifmmode\expandafter\tilde\else\expandafter\~\fi{A},$$ Young’s modulus E and area moment of inertia I is given by:

$$ EI\frac{{\partial ^{4} w{\left( {z,t} \right)}}} {{\partial z^{4} }} + \rho \ifmmode\expandafter\tilde\else\expandafter\~\fi{A}\frac{{\partial ^{2} w{\left( {z,t} \right)}}} {{\partial t^{2} }} = f_{{\text{S}}} {\left( {z,t} \right)}\; $$

(16)

The damping and added mass effects are included in the drag force f_S(z, t), which is described by the Stokes’ solution, see Eq. 15. For the above defined cantilever beam, the necessary boundary conditions to solve Eq. 16 are w|_{(z=0, t)}=0, ∂w/∂z|_{(z=0, t)}=0 for the clamped end at z=0 and ∂²w/∂z²|_{(z=L, t)}= 0, ∂³w/∂z³|_{(z=L, t)}=0 for the free end.

For the frequency response in the form of transverse vibrations, we assume a synchronous motion, which implies that the solution w(z, t) is separable in its spatial and temporal components. A particular solution of separated variables in t and z, i.e. the mode vibration η(t) and the mode shape Φ(z), is chosen as given in Eq. 17. It can be shown that the general solution can be expressed as a summation of all particular solutions:

$$ w_{{\text{i}}} {\left( {z,t} \right)} = \eta _{{\text{i}}} {\left( t \right)}\,\Phi _{{\text{i}}} {\left( z \right)} \to w{\left( {z,t} \right)} = {\sum\limits_{i = 1}^\infty {\eta _{i} {\left( t \right)}\Phi _{i} {\left( z \right)}} } $$

(17)

This solution procedure for Eq. 16 is called the normal mode expansion, in which the modes, i.e. the eigenfunctions, are obtained from the associated eigenvalue problem, i.e. the non-forced case. Then, Eq. 16 can be split into two equations for the time-dependent part η _i (t) and for the spatial dependence Φ _i (z):

$$ \begin{array}{*{20}l} {{{\text{non - forced:}}} \hfill} & {{\ifmmode\expandafter\ddot\else\expandafter\"\fi{\eta }_{i} + {\underbrace {{\left( {\frac{{EI\Phi _{{izzzz}} }} {{\rho \ifmmode\expandafter\tilde\else\expandafter\~\fi{A}\Phi _{i} }}} \right)}}_{{{\text{const}} = \omega ^{2}_{i} }}}\eta _{i} = 0} \hfill} \\ {{{\text{forced:}}} \hfill} & {{\ifmmode\expandafter\ddot\else\expandafter\"\fi{\eta }_{i} + \omega ^{2}_{i} \eta _{i} = \ifmmode\expandafter\tilde\else\expandafter\~\fi{C}_{i} {\int\limits_0^L {f{\left( {z,t} \right)}\Phi _{i} {\left( z \right)}\,{\text{d}}z} }\quad {\text{with}}\; \ifmmode\expandafter\tilde\else\expandafter\~\fi{C}_{i} = {\left( {\rho \ifmmode\expandafter\tilde\else\expandafter\~\fi{A}{\int\limits_0^L {\Phi ^{2}_{i} {\left( z \right)}{\text{d}}z} }} \right)}^{{ - 1}} } \hfill} \\ \end{array} $$

(18)

$$ \Phi _{{i\,zzzz}} - \frac{{\rho \ifmmode\expandafter\tilde\else\expandafter\~\fi{A}}} {{\,EI}}\omega ^{2}_{i} \Phi _{i} = 0 $$

(19)

The mode shapes Φ_i(z) are independent of the force approximation and can be determined from the non-forced case f(z, t)=0. Under the above constraints, the resulting mode shapes are determined (Volterra and Zachmanoglou 1965):

$$ \Phi _{i} {\left( z \right)} = \frac{1} {2}{\left\{ {\cos {\left( {\frac{{\lambda _{i} z}} {L}} \right)} - \cosh {\left( {\frac{{\lambda _{i} z}} {L}} \right)} + \ifmmode\expandafter\bar\else\expandafter\=\fi{C}_{i} {\left[ {\sin {\left( {\frac{{\lambda _{i} z}} {L}} \right)} - \sinh {\left( {\frac{{\lambda _{i} z}} {L}} \right)}} \right]}} \right\}} $$

(20)

where λ _i and $\ifmmode\expandafter\bar\else\expandafter\=\fi{C}_{{\text{i}}}$ are integration constants determined from the boundary conditions. Note that only the first few modes of vibration have significantly large amplitudes. In a first approximation, only the first mode Φ₁(z) is considered with λ₁=1.875 and $\ifmmode\expandafter\bar\else\expandafter\=\fi{C}_{1} = 0.734.$ In addition, since the system is analysed for the steady-state response, we assume a response with the same frequency dependence as the force in the form:

$$ U{\left( t \right)} = U_{0} \sin {\left( {\omega t} \right)} \to \eta _{1} {\left( t \right)} = H_{1} \sin {\left( {\omega t + \varphi _{1} } \right)} $$

(21)

Plugging the expression of the force given in Eq. 15 and the mode vibration given by Eq. 21 into Eq. 18, together with the first mode shape in Eq. 20, one obtains the following analytical expression for the amplitude H₁ and phase ϕ₁ of η₁(t):

$$ H_{1} = {\sqrt {\frac{{A^{2}_{1} + B^{2}_{1} }} {{{\left( {\omega ^{2}_{1} - \omega ^{2} - \omega C_{1} } \right)}^{2} + \omega ^{2} D^{2}_{1} }}} } $$

(22)

$$ \varphi _{1} = \tan ^{{ - 1}} {\left( {\frac{{{\left( {\omega ^{2}_{1} - \omega ^{2} - \omega C_{1} } \right)}B_{1} - \omega D_{1} A_{1} }} {{{\left( {\omega ^{2}_{1} - \omega ^{2} - \omega C_{1} } \right)}B_{1} + \omega D_{1} A_{1} }}} \right)} $$

(23)

with:

$$ A_{1} = \ifmmode\expandafter\tilde\else\expandafter\~\fi{C}_{1} {\int\limits_0^L {\,{\left| {Z_{{\text{S}}} {\left( z \right)}} \right|}U{\left( z \right)}\Phi _{1} {\left( z \right)}\cos {\left( {\zeta _{{\text{S}}} {\left( z \right)} + \xi _{{\text{S}}} {\left( z \right)}} \right)}{\text{d}}z} } $$

(24)

$$ B_{1} = \ifmmode\expandafter\tilde\else\expandafter\~\fi{C}_{1} {\int\limits_0^L {{\left| {Z_{{\text{S}}} {\left( z \right)}} \right|}U{\left( z \right)}\Phi _{1} {\left( z \right)}\sin {\left( {\zeta _{{\text{S}}} {\left( z \right)} + \,\xi _{{\text{S}}} {\left( z \right)}} \right)}{\text{d}}z} } $$

(25)

$$ C_{1} = \ifmmode\expandafter\tilde\else\expandafter\~\fi{C}_{1} {\int\limits_0^L {{\left| {Z_{{\text{S}}} {\left( z \right)}} \right|}\Phi ^{2}_{1} {\left( z \right)}\sin {\left( {\zeta _{{\text{S}}} {\left( z \right)}} \right)}{\text{d}}z} } $$

(26)

$$ D_{1} = \ifmmode\expandafter\tilde\else\expandafter\~\fi{C}_{1} {\int\limits_0^L {{\left| {Z_{{\text{S}}} {\left( z \right)}} \right|}\Phi ^{2}_{1} {\left( z \right)}\cos {\left( {\zeta _{{\text{S}}} {\left( z \right)}} \right)}{\text{d}}z} } $$

(27)

Finally, the deflection of the first-mode vibration of the beam in a steady-state response is given as:

$$ w_{1} {\left( {z,t} \right)} = \eta _{1} {\left( t \right)}\Phi _{1} {\left( z \right)} = H_{1} \sin {\left( {\omega t + \varphi _{1} } \right)}\Phi _{1} {\left( z \right)} $$

(28)

and the tip deflection amplitude reads as:

$$ w_{{\text{L}}} = H_{1} \Phi _{1} {\left( L \right)} $$

(29)